支持向量机
2019年3月1日已知点(2,3)、(4,5),求经过这两点的直线
法1:按照《如何求直线方程》
\[
k=\frac{5-3}{4-2}=1
\]
\[
\begin{align*}
y &=x+b \\
3 &= 2+b\\
b &= 1
\end{align*}
\]
所以直线为y=x+1,或x-y+1=0。
法2:按照《已知直线上两点求直线的一般式方程》
A=5-3=2
B=2-4=-2
C=3*4-5*2=2
所以直线为2x-2y+2=0。
疑问:法1和法2求出来的是同一条直线吗?
当然是相同的,法2的直线两边同除以2就得到法1的直线了。
但这种表示形式不是唯一的。若限制[latex]A\geqslant 0[/latex],及A、B、C最大公约数为1,则可以直线用唯一形式来表示。
若把直线方程Ax+By+C=0用向量形式表示,则有[latex]\vec{w}\cdot \vec{x}+C=0[/latex]。但这种表示形式也不是唯一的。对于一维直线,[latex]\vec{w}=\overrightarrow{(A, B)}[/latex],称为直线的法向量。
已知直线[latex](3,4)\cdot \vec{x}-1=0[/latex],求证[latex]\vec{w}=\overrightarrow{(3,4)}[/latex]为该直线的法向量。
设[latex]P_1=(x_1,y_1)[/latex]、[latex]P_2=(x_2,y_2)[/latex]在直线上,则有[latex](3,4)\cdot (x_1,y_1)-1=0[/latex],[latex](3,4)\cdot (x_2,y_2)-1=0[/latex]。
向量[latex]\overrightarrow{P_1P_2}=(x_2-x_1,y_2-y_1)[/latex]。
\[\begin{align*}
\overrightarrow{P_1P_2}\cdot \vec{w} &= (x_2-x_1,y_2-y_1) \cdot (3,4)\\
&= 3x_2-3x_1+4y_2-4y_1\\
&= 3x_2+4y_2 -(3x_1+4y_1) \\
&= 1 – 1 \\
&= 0
\end{align*}\]
所以[latex]\vec{w}[/latex]为直线的法向量。
解:
[latex]d=\frac{3\times 3+4\times 4 -1}{\sqrt{3^2+4^2}}=\frac{24}{5}[/latex],称此为点到直线的几何距离。
根据定义,设单位函数距离式为[latex]3nx+4ny-n=0[/latex],[latex][/latex]。
\[\begin{align*}
9n+16n-n =& 1 \\
n =& \frac{1}{24}
\end{align*}\]
所以,求直线3x+4y-1=0相对于点(3,4)的单位函数距离式为[latex]\frac{1}{8}x+\frac{1}{6}y-\frac{1}{24}=0[/latex]。
解:
用Mathematica,分四种条件计算。
anchorPoint = {3, 4};
k = Table[Tan[x], {x, 0, 2 Pi, 0.3}];
ContourPlot[ Evaluate[
Union[ Map[ {w1, 1}.{x, y} + b == 0 /. FindInstance[{ {w1, 1}.anchorPoint + b == 1, # == w1/1}, {w1, b}, Reals][[1]] &, k],
Map[ {w1, 1}.{x, y} + b == 0 /. FindInstance[{ {w1, 1}.anchorPoint + b == -1, # == w1/1}, {w1, b}, Reals][[1]] &, k],
Map[ {1, w2}.{x, y} + b == 0 /. FindInstance[{ {1, w2}.anchorPoint + b == 1, # == 1/w2}, {w2, b}, Reals][[1]] &, Table[Tan[x], {x, 0.1, 2 Pi, 0.3}]],
Map[ {1, w2}.{x, y} + b == 0 /. FindInstance[{ {1, w2}.anchorPoint + b == -1, # == 1/w2}, {w2, b}, Reals][[1]] &, Table[Tan[x], {x, 0.1, 2 Pi, 0.3}]]]],
{x, 1, 5}, {y, 2, 6},
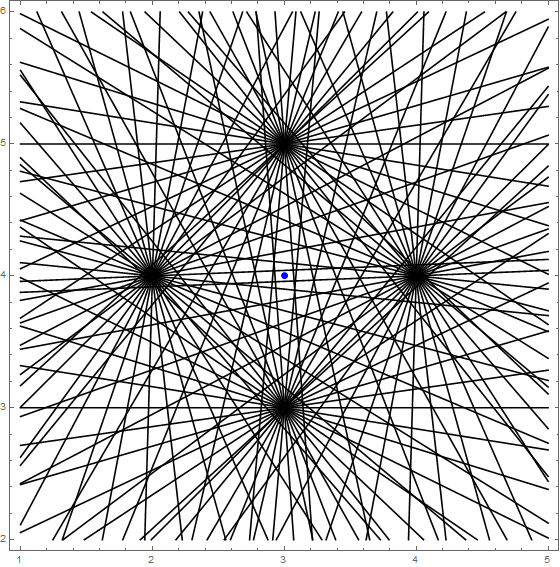
Epilog -> {Blue, PointSize@Large, Point[anchorPoint]} , ContourStyle -> Black ]如图可见,若x或y的系数为1,相对于点(3,4)的单位函数距离式必穿过(2,4)、(4,4)、(3,3)、(3,5)其中一点。
ContourPlot[ Evaluate[
Union[Map[ {w1, 2}.{x, y} + b == 0 /. FindInstance[{ {w1, 2}.anchorPoint + b == 1, # == w1/1}, {w1, b}, Reals][[1]] &, k],
Map[ {w1, 2}.{x, y} + b == 0 /. FindInstance[{ {w1, 2}.anchorPoint + b == -1, # == w1/1}, {w1, b}, Reals][[1]] &, k],
Map[ {2, w2}.{x, y} + b == 0 /. FindInstance[{ {2, w2}.anchorPoint + b == 1, # == 1/w2}, {w2, b}, Reals][[1]] &, Table[Tan[x], {x, 0.1, 2 Pi, 0.3}]],
Map[ {2, w2}.{x, y} + b == 0 /. FindInstance[{ {2, w2}.anchorPoint + b == -1, # == 1/w2}, {w2, b}, Reals][[1]] &, Table[Tan[x], {x, 0.1, 2 Pi, 0.3}]] ]],
{x, 2, 4}, {y, 3, 5},
Epilog -> {Blue, PointSize@Large, Point[anchorPoint]} , ContourStyle -> Black ]如图可见,若x或y的系数为2,相对于点(3,4)的单位函数距离式必穿过(2.5,4)、(3.5,4)、(3,3.5)、(3,4.5)其中一点。
以此类推,相对于点(3,4)的单位函数距离式必不穿过(3,4),必穿过(m,4)、(3,n)其中一点。
更进一步,相对于点(3,4)的单位函数距离式可穿过平面上除(3,4)外的任意一点。
第一层
现有样本集合X,每一个样本[latex]x_i[/latex]有类别[latex]y_i[/latex]。支持向量机处理的是二分类问题,所以设[latex]y_i[/latex]可以取两个值,传统上,设[latex]y_i\in \{+1, -1 \}[/latex]。
支持向量机求的是能把所有点正确分类,且对所有点距离最远的超平面。
设该超平面为[latex]\vec{w}\cdot \vec{x}+b=0[/latex]。
设有点[latex]p_1,p_1,\cdots, p_N[/latex],求离决侧面距离最近的点,离决侧面的距离是多少?
\[
d_{\text{min}}=\underset{1\leqslant n\leqslant N}{\min}\frac{y_n(\vec{w}\cdot \vec{x_n}+b)}{\left \| w \right \|}
\]
上式解释一下,通过变化n,令[latex]\frac{y_n(\vec{w}\cdot \vec{x_n}+b)}{\left \| w \right \|}[/latex]最小。n代表了该点的序号。设该点为[latex]p_{\text{min}}[/latex]。
但是决策面本身的性质要求它与所有点的距离最大,换句话说,决策面到离其最近的点的距离最大,即
\[
\begin{align}
& \underset{\vec{w},b}{\max}\ d_{\text{min}} \notag \\
=& \underset{\vec{w},b}{\max}\left\{ \underset{n}{\min}\left[\frac{y_n(\vec{w}\cdot \vec{x_n}+b)}{\left \| w \right \|}\right] \right\} \label{maxmin} \\
\end{align}
\]
上式解释一下,通过变化[latex]\vec{w}[/latex]和b,令[latex]d_{\text{min}}[/latex]最大。
若把超平面为[latex]\vec{w}\cdot \vec{x}+b=0[/latex]看成关于[latex]p_{\text{min}}[/latex]的单位函数距离式,则有[latex]d_{\text{min}}=\frac{1}{\left \| w \right \|}[/latex]
等式[latex]\eqref{maxmin} [/latex]可化简为[latex]\underset{\vec{w},b}{\max}\left( \frac{1}{\left \| w \right \|} \right)[/latex],相当于[latex]\underset{\vec{w},b}{\min}\left( \left \| w \right \| \right)[/latex]
考虑到[latex]\left \| \vec{w} \right \|=\sqrt{\sum w_i^2}[/latex],我们改为最小化[latex]\left \| \vec{w} \right \|^2[/latex]
考虑到对[latex]\left \| \vec{w} \right \|^2[/latex]求导会产生系数2,我们改为最小化[latex]\frac{1}{2}\left \| \vec{w} \right \|^2[/latex]。
\[\begin{equation}
f(\vec{w})=\frac{1}{2}\left \| \vec{w} \right \|^2
\label{目标函数}
\end{equation}\]
有人会说了,这个最小化问题非常简单,[latex]\vec{w}=(0, 0, \cdots, 0)[/latex]就最小了。不过,你忘了我们有约束条件。最小化[latex]\frac{1}{2}\left \| \vec{w} \right \|^2[/latex]的同时,还必须保证所有点正确分类呀。
所以最小化[latex]\frac{1}{2}\left \| \vec{w} \right \|^2[/latex]时的约束条件为
\[\begin{equation}
\forall x_i,y_i \quad y_i(\vec{w}\cdot \vec{x_i}+b)\geqslant 1
\label{原始限制条件}
\end{equation}\]
。
如果你读到现在,恭喜你,你已经打通了SVM第一层!
第二层
拉格朗日函数
拉格朗日函数非常简单,非常简单,非常简单!!!重要的事情说三遍。不要看到天书般的名词就害怕了。
\[
\underset{x}{\min}\ f(x) \qquad
\text{满足}
c_i(x)\leqslant 0 \forall i\in \{1,2,\cdots, N\}
\]
,则拉格朗日函数把以上两式合并起来
\[
L(x,\boldsymbol{\alpha})=f(x)+\sum_{i=1}^{N}\alpha_ic_i(x)
\]
\[
(\alpha_i \geqslant 0 \ \forall i \in \{1,2,\cdots, N\})
\]
注意,上面[latex]\boldsymbol{\alpha}[/latex]是粗体,表示一个集合。
没了,是不是非常简单!!!
假设[latex]c_u(x)[/latex]不满足条件,即[latex]c_u(x)>0[/latex],我们都可以通过调整[latex]\alpha_u \ (\alpha_u>0)[/latex],令[latex]L(x,\boldsymbol{\alpha}) \rightarrow +\infty[/latex]。
但是如果满足满足原始问题的限制条件,拉格朗日函数退化为[latex]L(x,\boldsymbol{\alpha})=f(x)[/latex]。
拉格朗日函数是不是既精妙又简单!!!
通过上面的分析我们知道,拉格朗日函数一不小心就会出现正无穷,我们来试试求它的最小值。
首先,通过改变[latex]\boldsymbol{\alpha}[/latex]最大化[latex]L(x,\boldsymbol{\alpha})[/latex],测试是否有点不符合约束条件。
然后,在满足约束条件的情况下,改变x,求拉格朗日函数的最小值。以上过程可表示为
\[
\underset{x}{\min}\ \underset{\boldsymbol{\alpha}}{\max} \ L(x,\boldsymbol{\alpha})
\]
这叫做拉格朗日极小极大问题。
我们再看极小极大问题的对偶问题——极大极小问题:
\[
\underset{\boldsymbol{\alpha}}{\max} \ \underset{x}{\min}\ L(x,\boldsymbol{\alpha})
\]
极小极大问题和极大极小问题被认为是等价的,证明从略。
现在,将公式\eqref{原始限制条件}变形
\[\begin{align}
\forall x_i,y_i \quad & & y_i(\vec{w}\cdot \vec{x_i}+b) & \geqslant 1 \notag \\
& & -y_i(\vec{w}\cdot \vec{x_i}+b) & \leqslant -1 \notag \\
& & -y_i(\vec{w}\cdot \vec{x_i}+b)+1 & \leqslant 0 \label{拉格朗日不等式} \\
\end{align}\]
于是公式[latex]\eqref{目标函数}[/latex]符合拉格朗日函数的目标函数形式,公式[latex]\eqref{拉格朗日不等式}[/latex]符合拉格朗日函数的不等式形式。将它们代入拉格朗日函数,得
\[
\begin{align}
L(x,\boldsymbol{\alpha}) =& \frac{1}{2}\left \| \vec{w} \right \|^2-\sum_{i=1}^{N}\alpha_i (y_i(\vec{w}\cdot \vec{x_i}+b)-1) \notag \\
=& \frac{1}{2}\left \| \vec{w} \right \|^2-\sum_{i=1}^{N}\left(\alpha_i y_i \vec{w}\cdot \vec{x_i} +\alpha_i y_i b-\alpha_i \right) \label{拉格朗日展开式} \\
\end{align}
\]
求[latex]f(\vec{w})[/latex]的最小值变成了求L的最小值。当L取最小值时,L对[latex]\vec{w}[/latex]和b的偏导数必为0,即
\[\begin{gather}
\frac{\partial L}{\partial \vec{w}}=\vec{w} – \sum_{i=1}^{N}\alpha_i y_i\vec{x_i}=0 \notag \\
\vec{w} = \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \label{w偏导数} \\
\frac{\partial L}{\partial b}= \sum_{i=1}^{N}\alpha_i y_i=0 \label{b偏导数} \\
\end{gather}\]
把[latex]\eqref{w偏导数}\text{、}\eqref{b偏导数}[/latex]反代回[latex]\eqref{拉格朗日展开式}[/latex],得
\[
\begin{align*}
L(x,\boldsymbol{\alpha}) =& \frac{1}{2}\left \| \color{Red}{ \vec{w}} \right \|^2-\sum_{i=1}^{N}\left(\alpha_i y_i \vec{w}\cdot \vec{x_i} +\alpha_i y_i b-\alpha_i y_i \right) & \text{红色部分为应用公式\eqref{w偏导数}} \\
=& \frac{1}{2}\left ( \color{Red}{\sum_{i=1}^{N}\alpha_i y_i\vec{x_i}} \right )^2-\sum_{i=1}^{N} \left( \alpha_i y_i\color{Red}{\vec{w}}\vec{x_i} +\alpha_iy_ib-\alpha_i \right) \\
=& \frac{1}{2}\left ( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right )^2-\sum_{i=1}^{N} \left( \alpha_i y_i\left( \color{Red}{ \sum_{i=1}^{N}\alpha_i y_i\vec{x_i}} \right)\vec{x_i} \right) – b\color{Blue}{\sum_{i=1}^{N}\alpha_iy_i} + \sum_{i=1}^{N}\alpha_i & \text{蓝色部分为应用公式\eqref{b偏导数}} \\
=& \frac{1}{2}\left ( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right )^2-\sum_{i=1}^{N} \left( \alpha_i y_i\vec{x_i}\left( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right) \right) – b\times \color{Blue}{0} + \sum_{i=1}^{N}\alpha_i \\
=& \frac{1}{2}\left ( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right )^2-\left( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right)\sum_{i=1}^{N} \left( \alpha_i y_i\vec{x_i} \right) + \sum_{i=1}^{N}\alpha_i \\
=& \frac{1}{2}\left ( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right )^2-\left( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right)^2 + \sum_{i=1}^{N}\alpha_i \\
=& \sum_{i=1}^{N}\alpha_i – \frac{1}{2}\left ( \sum_{i=1}^{N}\alpha_i y_i\vec{x_i} \right )^2\\
\end{align*}
\]
参考资料
https://zhuanlan.zhihu.com/p/31886934
https://blog.csdn.net/v_JULY_v/article/details/7624837
https://zhuanlan.zhihu.com/p/24638007
https://zhuanlan.zhihu.com/p/34811858
\[
\underset{x}{\min}\ f(x) \qquad
\text{满足}
\begin{cases}
c_i(x)\leqslant 0 & \forall i\in \{1,2,\cdots, N\} \\
h_j(x)= 0 & \forall j\in \{1,2,\cdots, L\}
\end{cases}
\]
,则拉格朗日函数把以上三式合并起来
\[
L(x,\boldsymbol{\alpha},\boldsymbol{\beta})=f(x)+\sum_{i=1}^{N}\alpha_ic_i(x)+\sum_{j=1}^{L}\beta_jh_j(x)
\]
\[
\alpha_i \geqslant 0 \ \forall i \in \{1,2,\cdots, N\}
\]
\[
-\infty < \beta_j <+\infty \ \forall j \in \{1,2,\cdots, L\}
\]
注意,上面[latex]\boldsymbol{\alpha},\boldsymbol{\beta}[/latex]是粗体,表示一个集合。
没了,是不是非常简单!!!
从观察可知,拉格朗日函数要求[latex]\alpha[/latex]大于0,而对[latex]\beta[/latex]没有要求。
假设[latex]c_u(x)[/latex]不满足条件,即[latex]c_u(x)>0[/latex],我们都可以通过调整[latex]\alpha_u \ (\alpha_u>0)[/latex],令[latex]L(x,\boldsymbol{\alpha},\boldsymbol{\beta}) \rightarrow +\infty[/latex]。
假设[latex]h_v(x)[/latex]不满足条件,即[latex]h_v(x)\neq 0[/latex],我们都可以通过调整[latex]\beta_v \ (\beta_v \text{无范围限制})[/latex],令[latex]L(x,\boldsymbol{\alpha},\boldsymbol{\beta}) \rightarrow +\infty[/latex]。
但是如果满足满足原始问题的限制条件,拉格朗日函数退化为[latex]L(x,\boldsymbol{\alpha},\boldsymbol{\beta})=f(x)[/latex]。
拉格朗日函数是不是既精妙又简单!!!
通过上面的分析我们知道,拉格朗日函数一不小心就会出现正无穷,我们来试试求它的最小值。
首先,通过改变[latex]\boldsymbol{\alpha},\boldsymbol{\beta}[/latex]最大化[latex]L(x,\boldsymbol{\alpha},\boldsymbol{\beta})[/latex],测试是否有点不符合约束条件。
然后,在满足约束条件的情况下,改变x,求拉格朗日函数的最小值。以上过程可表示为
\[
\underset{x}{\min}\ \underset{\boldsymbol{\alpha},\boldsymbol{\beta}}{\max} \ L(x,\boldsymbol{\alpha},\boldsymbol{\beta})
\]
这叫做拉格朗日极小极大问题。
我们再看极小极大问题的对偶问题——极大极小问题:
\[
\underset{\boldsymbol{\alpha},\boldsymbol{\beta}}{\max} \ \underset{x}{\min}\ L(x,\boldsymbol{\alpha},\boldsymbol{\beta})
\]
极小极大问题和极大极小问题被认为是等价的,证明从略。
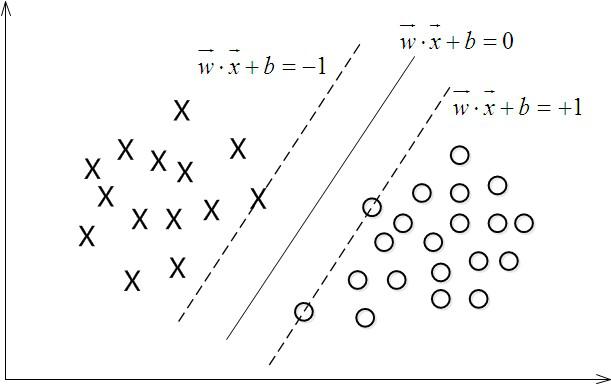
从观察可知,l仅由两个不同类得边界分割面所穿过得点决定,如上图的1个X,两个O。两个不同类得边界分割面所穿过得点称为支持向量。
所有的支持向量[latex]x_i[/latex]到超平面l的距离都相同,可设为d。
由定理1,始终存在w和b,令
\[\begin{equation}
\forall x_i \quad \left|\vec{w}^\top\vec{x_i}+b\right|=1
\label{绝对值1}
\end{equation}\]
。
考虑到每个[latex]x_i[/latex]都有分类[latex]y_i[/latex],且[latex]y_i\in \{+1, -1 \}[/latex]。可做如下假设
\[
\begin{equation}
y_i=\begin{cases}
+1 & \text{若 } \vec{w}^\top\vec{x_i}+b\geqslant 1\\
-1 & \text{若 } \vec{w}^\top \vec{x_i}+b <1 \\
\end{cases}
\label{y的分类}
\end{equation}
\]
可以对公式[latex]\eqref{y的分类}[/latex]进行归一化处理,得
\[
y_i(\vec{w}^\top\vec{x_i}+b)\geqslant 1
\]
根据《向量复习》,任意一点到该决策面的距离为 [latex]d=\frac{\left| \vec{w}^\top\vec{x} \right |}{\left \| \vec{w} \right \|}[/latex]。对于支持向量[latex]x_i[/latex],则有
\[\begin{equation}
d=\frac{1}{\left \| \vec{w} \right \|}
\end{equation}\]
为了最大化d,需要最小化[latex]\left \| \vec{w} \right \|[/latex]。
怎么把“能把所有点正确分类”用数学表示呢?
对任意一点[latex](\vec{x_i},y_i)[/latex],将[latex]x_i[/latex]代入l,
当然,如果写成
\[
y_i=\begin{cases}
+1 & \text{ 若} \vec{w}^\top\vec{x_i}+b\leqslant 0 \\
-1 & \text{ 若 } \vec{w}^\top\vec{x_i}+b>0
\end{cases}
\]
也可以。只是[latex]\vec{w}[/latex]的符号相反而已。
通过放大缩小[latex]\vec{w}[/latex]和[latex]\vec{b}[/latex],可以对公式[latex]\eqref{y的分类}[/latex]进行归一化处理,得
若对公式[latex]\eqref{y的分类}[/latex]进行简单合并,得到的是[latex]y_i(\vec{w}^\top\vec{x_i}+b)\geqslant 0[/latex]。待办:使用此公式进行推导。
如果该决策面能对所有点进行正确分类,则一定有[latex]\forall (\vec{x_i},y_i),\ y_i(\vec{w}^\top\vec{x_i}+b)\geqslant 1[/latex]
如果限制[latex]A\geqslant 0[/latex],且[latex]A^2+B^2=1[/latex],也可以把直线用唯一形式来表示。
若限制[latex]\vec{w}[/latex]正规化为单位向量,即[latex]\left\| \vec{w} \right\|=1[/latex],则可以把直线用唯一形式来表示。注意,因为[latex]\vec{w}[/latex]正规化了,C也会改变。注意,本文将通篇使用向量形式来表示直线(和超平面),并要求[latex]\vec{w}[/latex]为单位向量。