题目来自https://oj.leetcode.com/problems/fraction-to-recurring-decimal/。

Given two integers representing the numerator and denominator of a fraction, return the fraction in string format.

If the fractional part is repeating, enclose the repeating part in parentheses.

For example,

• Given numerator = 1, denominator = 2, return “0.5”.
• Given numerator = 2, denominator = 1, return “2”.
• Given numerator = 2, denominator = 3, return “0.(6)”.

看了这道题，我第一个想法是能不能用编程语言自带的除法算出双精度小数，然后用正则表达式提取循环部分。

正则表达式

假设分子分母分别为1和11，Java算出小数为0.09090909090909091。人眼看出循环节为09，小数最后一位由于精度问题不准确，会干扰正则匹配，所以匹配前予以去除。此外，小数点前的部分不属于循环节，也要去除。

现在，设计一个正则表达式，求出596363636的循环节。

这里的59是循环小数的非循环部分，可用.*?跳过。

然后应该捕获字符串，并继续匹配，知道后面重现已经捕获的字符串，这就表示一个循环节走完了。

(?<s>\d+?)(?<t>((?!\k<s>).)*)(\k<s>\k<t>)*\k<s>$

(?<s>\d+?)为命名为s（start，循环节的开始部分）的捕获组，匹配一个或多个数字。正则表达式末尾反向引用s捕获组（\k<s>），表示小数的最后部分应该以循环节的开头一部分结尾。

比如03703703703，循环节为037。小数最后03是循环节的开头部分，这时捕获组k=”03″。

捕获组s之后，是捕获组t（tail，结尾，(?<t>((?!\k<s>).)*)）。捕获组s和t共同构成了整个循环节。这个地方重点解释一下。

表达式的有宽和零宽

正则表达式里面，如\d、.等是占有字符的（消费字符的、消耗字符的，有宽度的），它会驱动正则引擎将正则的后续部分与字符串的后续部分继续匹配。

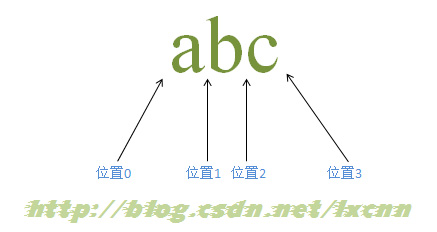
各种零宽断言不是匹配字符，而是匹配位置，所以对于对于字符来说它们是零宽的。对于字符串“abc”而言，包括三个字符和四个位置。

 

图片转载自《正则基础之——NFA引擎匹配原理》^[1]

(?!\k<s>)是零宽度负预测先行断言——这名称非常拗口，只要记住1、是零宽的；2、断言此位置的后面不能匹配表达式^[2]。由于这是零宽断言，并不“消费”字符，引擎不继续匹配字符串的剩余部分。所以后面要加.，让引擎前进一个字符。

((?!\k<s>).)*整个的意思就是，如果一个位置后面的字符串不匹配s组，则前进一个字符。前进得越多越好，直到一个位置后面的字符匹配s组；也可以不前进（如果用+而不是*，就至少前进一个字符）。

这部分表达式匹配完，正则引擎应该已经走完了整个循环节，后面应该是0个或多个循环节（(\k<s>\k<t>)*）加1个循环节的开始部分（\k<s>$）。

在后来的测试中我逐渐发现，在某些情况下（如除数比被除数大很多），小数有较长的非循环部分或者有较长的循环部分。我就怀疑它们到底能否用双精度小数的16位十进制有效数字表示。

循环小数的性质

循环小数的非循环长度和循环长度跟除数与被除数到底有什么关系呢？

• 一个分母为N的循环小数的循环节位数最多不超过N-1位。（性质一）
• 除数a为[latex]2^p 5^q[/latex]的倍数时，[latex]1\div a[/latex]有max(p,q)个不循环位数。^[3]
• 若n为非循环长度，r为循环长度，除数a不是2或5的倍数，则[latex]10^n(10^r-1)[/latex]可以被a整除。

由此我们得出计算非循环长度和循环长度的步骤：

1. 给定任意整数a、b，化为最简假分数形式[latex]c\frac{a’}{b’}[/latex]（a’、b’互质）。
2. 对a’进行因数分解，[latex]a’=2^p 5^q a^{\prime\prime}[/latex]，所以得到非循环长度为n=max(p,q)。
3. （用线性搜索或其他技巧）寻找令[latex]10^n(10^r-1) \equiv 0 \pmod{a^{\prime\prime}}[/latex]成立的最小的r，r就是循环节长度。

例子

求解[latex]994\div 596[/latex]的非循环长度和循环长度。

[latex]994\div 596=\frac{497}{298}=1\frac{199}{298}[/latex]。整数部分为1，现在我们求[latex]\frac{199}{298}[/latex]的非循环长度和循环长度。

对298因数分解，得[latex]2^1\times 149[/latex]。所以非循环长度为1。

下面寻找令[latex]10^n(10^r-1) \equiv 0 \pmod{a^{\prime\prime}}[/latex]成立的最小的r。当然可以暴力搜索法，如果用编程语言实现的话，很容易溢出（可能用BigInteger之类的类会好一点）。为了论证此过程，我这里用Mathematica。

[MathematicaIn n=””/]Reduce[Mod[10^1 (10^r – 1), 149] == 0, r, Integers][MathematicaOut n=””/][latex]c_1\in \mathbb{Z}\land c_1\geq 0\land r=148 c_1[/latex][latex]c_1[/latex]为常数

[MathematicaIn/]Minimize[{148 C[1], C[1]>0},C[1], Integers][MathematicaOut/]{148,{C[1]->1}}

于是得出r=148。再用Mathematica验算一下：

[MathematicaIn/]N[994/596, 200][MathematicaOut/]1.6677852348993288590604026845637583892617449664429530201342281879194630872483221476510067114093959731543624161073825503355704697986577181208053691275167785234899328859060402684563758389261744966442953
粗红部分就是循环节。

Mathematica的算法核心在Reduce函数，我自己怎么实现呢？

从维基百科^[4]看到，令[latex]a^d \equiv 1 \pmod{m}[/latex]成立的最小的d一定小于等于模m的原根，而模m的原根等于[latex]\varphi (m)[/latex]（[latex]\varphi[/latex]为欧拉函数）。

欧拉函数表示的是小于或等于m的正整数中与m互质的数的数目，这不是易求的，没有简单的函数可以求出。

如果没有欧拉函数，我们也可以利用性质一进行搜索，这就需要O(n)的时间，与其这样还不如直接求出小数。

最终解法

用短除法做除法我们都会，这里好好考虑一下什么情况时才算另一节循环节已经开始。

是出现重复的商了吗？不是！短除法一个位置的商只有0到9共9种可能，而除数并不限定在10以内。

是出现重复的余数了吗？余数跟除数其实并不做任何运算，真正决定商的是被除数。所以，如果被除数重复，我们就知道新的循环节开始了。

[code lang=”Java” gutter=”true”]
public String fractionToDecimal2(int numerator, int denominator)
{
return fractionToDecimal2(numerator, denominator, 0);
}

public String fractionToDecimal2(int numerator, int denominator, int moreDigits)
{
if (moreDigits < 0)
throw new IllegalArgumentException("参数moreDigits必须大于等于0。");

if (numerator == 0)
return "0";
else if (denominator == 0)
throw new ArithmeticException("分母为0。");
else if (numerator == Integer.MIN_VALUE && denominator == -1)
return "2147483648";// 此数超过Integer.MAX_VALUE，所以特殊处理。
else if (numerator == Integer.MIN_VALUE || // 没有其他int的绝对值可以大于 2147483648。
Math.abs(numerator) >= Math.abs(denominator))
{
DivisionResult d = divide(numerator, denominator);
if (d.getRemainder() != 0)
{
String val = fractionToDecimalLessThan1(d.getRemainder(), denominator, moreDigits);
int decimalPointIndex = val.indexOf(‘.’);
assert decimalPointIndex == 1 || decimalPointIndex == 2;
return d.getQuotient() + val.substring(decimalPointIndex);
}
else
return String.valueOf(d.getQuotient());
}
else
return fractionToDecimalLessThan1(numerator, denominator, moreDigits);
}

/**
* 返回小于1的小数。
*
* @param numerator
* @param denominator
* @return 0.XXXXX
*/
public String fractionToDecimalLessThan1(int numerator, int denominator, int moreDigits)
{
assert moreDigits >= 0;
assert numerator != 0 && denominator != 0;
assert Math.abs(numerator) < Math.abs(denominator) || denominator == Integer.MIN_VALUE :
"分子的绝对值必须小于分母的绝对值";
// assert numerator > 0 && denominator > 0 : "分子分母必须大于0";

StringBuilder sb = new StringBuilder();

// 被除数决定商。如果被除数重复，那么一节循环节已经结束。
LinkedHashSet<Long> dividends = new LinkedHashSet<>();
// dividends.add(numerator);
sb.append("0.");
long longNumerator = numerator * 10;
DivisionResult d;
boolean foundPeriod = false;

do
{
if (foundPeriod == false)
{
if (dividends.contains(longNumerator))
{ // 这个被除数之前已经出现过了，说明已经进入了第二个循环节

int periodStartIndex = 0;
for (long value : dividends)
{
if (value == longNumerator)
break;
periodStartIndex++;
}

assert periodStartIndex != -1 && periodStartIndex < dividends.size();
sb.insert(periodStartIndex + 2, "(");
sb.append(")");

foundPeriod = true;
}
else
dividends.add(longNumerator);
}

if (dividends.size() % 1000 == 0)
System.out.println("remainderIndexes.size()=" + dividends.size());

if (foundPeriod && moreDigits– == 0)
{
if (numerator < 0 && denominator > 0 || numerator > 0 && denominator < 0)
return "-" + sb.toString();
else
return sb.toString();
}

d = divide(longNumerator, denominator);
assert 0 <= Math.abs(d.getQuotient()) && Math.abs(d.getQuotient()) < 10;
sb.append(Math.abs(d.getQuotient()));

longNumerator = d.getRemainder() * 10l;
} while (d.getRemainder() != 0);

if (numerator < 0 && denominator > 0 || numerator > 0 && denominator < 0)
return "-" + sb.toString();
else
return sb.toString();
}

/**
*
* @param numerator
* 不得不为long，因为短除法中余数乘以10变成被除数，余数可能Integer.max。
* @param denominator
* @return
*/
private static DivisionResult divide(long numerator, int denominator)
{
int quotient = (int) (numerator / denominator);
int remainder = (int) (numerator – denominator * quotient);

return new DivisionResult(quotient, remainder);
}
[/code]

[code lang=”Java”]
class DivisionResult
{

private int quotient;

private int remainder;

public DivisionResult(int quotient, int remainder)
{
this.quotient = quotient;
this.remainder = remainder;
}

/**
* 获取商。最大值为2^32=Integer.MIN_VALUE/-1。
*
* @return
*/
public int getQuotient()
{
return quotient;
}

/**
* 获取余数。-2^32-1到2^32-2。
*
* @return
*/
public int getRemainder()
{
return remainder;
}

@Override
public boolean equals(Object obj)
{
if (obj instanceof DivisionResult)
{
DivisionResult other = (DivisionResult) obj;
return quotient == other.quotient && remainder == other.remainder;
}
else
return false;
}

@Override
public int hashCode()
{
if (quotient == 0)
return (int) remainder;
else
{
int length = (int) Math.log10(quotient);
assert length >= 0 && length <= 9;
int h = (int) (quotient * Math.pow(10, 9 – length));

return (int) (h + remainder);
}
}

@Override
public String toString()
{
return "q=" + quotient + ", r=" + remainder;
}
}
[/code]

为了调试方便，fractionToDecimal有两个重载，一个重载接受参数moreDigits，用来在循环节结束后计算更多的数字，用来验证循环节对不对。比如moreDigits=5，则输出0.8(63)63636。

还有一个重点是int的正负范围是不一样的。

核心部分在fractionToDecimalLessThan1方法。很多人用HashMap记录被除数和索引；但我用LinkedHashSet，它既可以O(1)时间获取元素，又记录元素的插入顺序，所以不用再显式记录索引了。

在do循环外面，要不要记录原始的被除数（第54行）？被除数决定商，原始的被除数决定个位的商，而由于方法本身的意义，个位商必为0，我这里也写死了（第55行）。 另外，个位的商不属于循环节，怎么能混入记录循环节的dividends里去呢？所以不该记录！

然后，见到重复的被除数说明新的循环节已经开始，按LeetCode的题目要求已经可以返回了。

所以循环里的操作顺序是：

1. 记录被除数
2. 做除法
3. 商加入到小数
4. 余数乘以10作新的被除数

参考资料

1. -过客-. 正则基础之——NFA引擎匹配原理. . 2009-06-28 [2015-01-04].↑
2. deerchao. 正则表达式30分钟入门教程. . 2013-01-10 [2015-01-04].↑
3. . 循环小数. 维基百科. [2015-01-04].↑
4. . 原根. 维基百科. [2015-01-04].↑