Minimum Cost to Make Array Equalindromic
2024年5月9日错误解法
Let nums = x_i.
Change all \(x_i\) to y, find the minimum value of \(\Sigma |x_i-y|\),
where y is palindromic, y > 0.
Rather than finding \(\Sigma |x_i-y|\), we find \(\Sigma (x_i-y)^2\).
Sigma (x_i-y)^2
= Sigma (x_i^2 + y^2 – 2x_iy)
= Sigma (x_i^2) + ny^2 – 2y Sigma (x_i)
Sigma (x_i^2) does not change. We only need to minimize ny^2 – 2y Sigma (x_i).
Rather than minimizing ny^2 – 2y Sigma (x_i), we minimize (ny^2 – 2y Sigma (x_i))/n.
(ny^2 – 2y Sigma (x_i))/n
= y^2 – 2y Sigma (x_i)/n
Sigma (x_i)/n is the average. Let is be the variable a. Then we get y^2 – 2ya.
y^2 – 2ya = y(y-2a)
This is a parabola, opens upward, axis at y = a.
Therefore as long as we find the palindromic number closest to the average, the problem is solved.
错误原因
平均数并不令absolute error最小。
举例来说,设有数列1,1,100。平均数为34,absolute error为135。中位数为1,absolute error为99。
中位数
中位数能否令absolute error最小?这是经典的Mean absolute error问题,也是median的性质之一。以下证明之。
For f(x), its minimal (maximal) value is at where its slope is 0.
Let \(f_1(x)=3x+7, f_2(x)=5x-4, f_3(x)=-2x-8\), their slopes are 3, 5, -2, respectively.
The slope of \(f_1(x)+f_2(x)+f_3(x)\) is 3+5-2.
Then we study absolute values.
Let \(f_1(x)=|x-2|,f_2(x)=|x+1|,f_3(x)=|x-3|\), what’s the slope of \(f(x)=f_1(x)+f_2(x)+f_3(x)\)?

Plot[Abs[x - 2], {x, -5, 5}]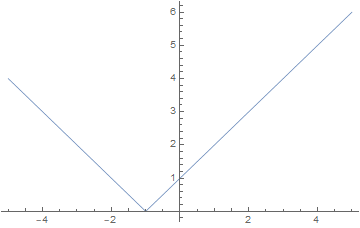
Plot[Abs[x + 1], {x, -5, 5}]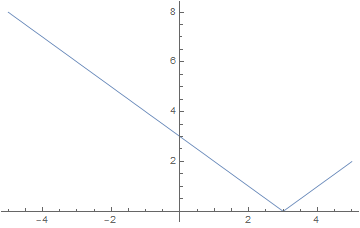
Plot[Abs[x - 3], {x, -5, 5}]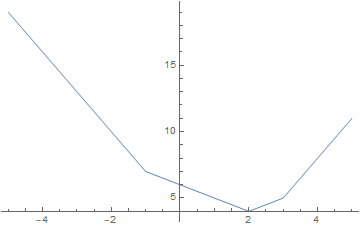
Plot[Abs[x - 2] + Abs[x + 1] + Abs[x - 3], {x, -5, 5}]We just need to check a few points.
When x=-1, \(f_1’=-1, f_2’=0, f_3’=-1, f’=-2\).
When x=2, \(f_1’=0, f_2’=1, f_3’=-1, f’=0\).
When x=3, \(f_1’=1, f_2’=1, f_3’=0, f’=2\).
Simply put, the overall slope is 0 when the slopes of subitems cancel each other. If we sort items, the slope of the combined function is 0 at median where there are the same number of items less than and greater than the prediction.
. Lecture 2 – Minimizing Mean Absolute Error. UC San Diego. [2024-05-09].
[…] Minimum Cost to Make Array Equalindromic […]