799. Champagne Tower

Use C to present Cup and \(C_{i,j}\) to present the fullness of the cup.

Law of Shape: \(C_{i,j}\) exists if i>=0, 0<j<=i.

Use \(I_{i,j}\) to present the income of \(C_{i,j}\), assuming relevant cups are full.

Laws of Income:
$$
I_{0,0}=1
$$

$$
I_{i,j}=
\begin{cases}
\frac{1}{2}I_{i-1,j} & \text{if}\ j=0 \\
\frac{1}{2}I_{i-1,j-1} + \frac{1}{2}I_{i-1,j} & \text{if}\ i>j>0 \\
\frac{1}{2}I_{i-1,j} & \text{otherwise}
\end{cases}
$$

To directly calculate the income of \(C_{i,j}\) from i’-th row. Let d=i-i’. Use the following equation. 0<=d<=j<=i'. $$ I_{i,j}= \left\{ \begin{array}{lll} \frac{?}{2^{i-i'}} I_{i',j-d}+\cdots+ I_{i',j} & \text{ i.e. } i-i'+1 \text{ items} & \text{ if } 0\leqslant d\leqslant j,\ j \leqslant i' \\ \frac{?}{2^{i-i'}} I_{i',0}+\cdots+ I_{i',j} & \text{ i.e. } j+1 \text{ items} & \text{ if } 0\leqslant j<d,\ j\leqslant i' \\ \frac{?}{2^{i-i'}} I_{i',j-d}+\cdots+ I_{i',i'} & \text{ i.e. } i-j+1 \text{ items} & \text{ if } 0\leqslant d\leqslant j,\ i'< j \\ \frac{?}{2^{i-i'}} I_{i',0}+\cdots+ I_{i',i'} & \text{ i.e. } i'+1 \text{ items} & \text{ if } 0\leqslant j<d,\ i'< j \end{array}\right. $$

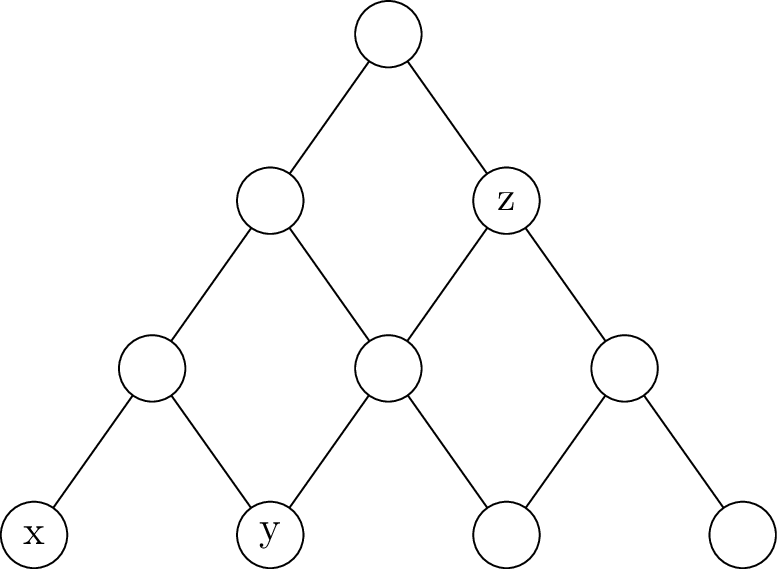
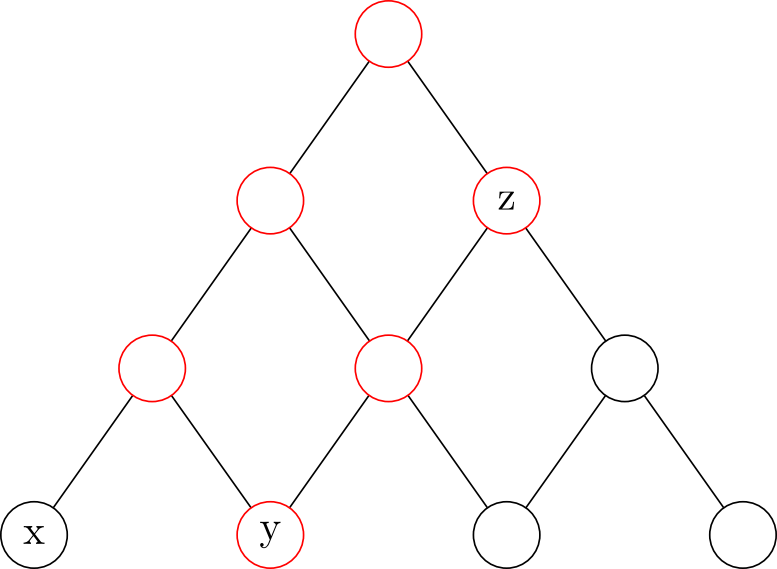
There is another point of view. The income of x is clearly \(\frac{1}{2}^3\). To find out the income of y, we can view y as part of the tree starting from z. What’s more, z receive income from its parent \(I_{2,0}\). \(I_{1,0}\) and \(I_{0,0}\) also contribute to the tree of z.

$$
I_{3,1}=\frac{1}{2}I_{2,0}+\frac{1}{2}I_{1,0}\frac{1}{2}+\frac{1}{2}I_{0,0}\frac{1}{2}^2
$$

Therefore the general form is

$$
I_{i,j}=\sum_{i’=i-1}^0 \frac{1}{2}^{i-i’} I_{i’,j-1}
$$

Property of Pouring

Assume we pour \(w_1\) glasses of water. \(w_1\) needs to fill the top cup, then overflows from both sides.

Hence, Cup 1,0 receives \(w_2=(w_1-1)/2\) glasses of water. \(w_2\) needs to fill the top cup, then overflows from both sides.

Hence, Cup 2,0 receives \(w_3=(w_2-1)/2\) glasses of water. \(w_3\) needs to fill the top cup, then overflows from both sides. So on and so forth.

$$
\begin{align*}
w_1 &= w_1 \\
w_2 &= \frac{1}{2}(w_1-1) = \frac{1}{2}w_1- \frac{1}{2} \\
w_3 &= \frac{1}{2}(w_2-1) = \frac{1}{2}(\frac{1}{2}w_1- \frac{1}{2} -1) = \frac{1}{4}w_1 – \frac{1}{4} – \frac{1}{2} \\
w_4 &= \frac{1}{2}(w_3-1) = \frac{1}{2}(\frac{1}{4}w_1 – \frac{1}{4} – \frac{1}{2} -1) = \frac{1}{8}w_1 – \frac{1}{8} – \frac{1}{4} – \frac{1}{2} \\
w_5 &= \frac{1}{2}(w_4-1) = \frac{1}{2}(\frac{1}{8}w_1 – \frac{1}{8} – \frac{1}{4} – \frac{1}{2} -1) = \frac{1}{16}w_1 – \frac{1}{16} – \frac{1}{8} – \frac{1}{4} – \frac{1}{2} \\
& \vdots \\
w_n &= \frac{1}{2}(w_{n-1}-1) = \frac{1}{2}^{n-1} w_1 – \sum_i^{n-1} \frac{1}{2}^i \quad \text{ provided } w_{n-1}>1
\end{align*}
$$

This sequence terminates when \(w_n\leqslant 1\), ie. \(1 < w_{n-1}\leqslant 3\).

\(\sum_i^{n-1} \frac{1}{2}^i\) 是一个等比数列。求和公式为\(1- \frac{1}{2}^n\). Therefore \(w_n = \frac{1}{2}^{n-1} w_1 – \sum_i^{n-1} \frac{1}{2}^i = \frac{1}{2}^{n-1} w_1 + \frac{1}{2}^{n-1} -1\).

Given \(w_1\), how to find n such that \(1 < w_{n-1}\leqslant 3\)?

Paths to target cup

Nodes affect y are highlited in red. These nodes form a rectangle.

How many paths are there to the target cup? This is a combination problem. Starting from the top node, you can plan your path from 2 left and 1 right. You take 3 actions in total and 1 action is right. So the number of paths is \(C_3^1=3\).