Manacher最长回文算法
2015年2月3日本文将一步一步构造Manacher算法,心急的一定看不懂!请先练习下面的习题。
探索最长回文串性质
题1:已知字符串以center为中心对称,求完整的字符串。
abcd??? | center
答
abcdcba | center
题2:接上题,abcdcba后面还有一些字符,以center2为中心,最大对称半径[1]为7,求完整的字符串。
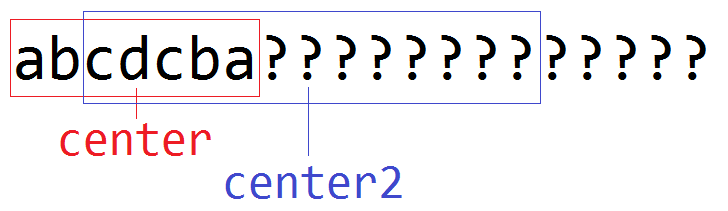
答
根据center2的对称性质,可以知道字符串为
abcdcba???abcdcb??
又根据center2最大对称半径为7,而不是8,所以c后面一定不是b(标识为b)。center3的对称半径确定!而且,center关于center2的对称点center3的索引号为center2*2-center=8*2-3=13。对称半径为center2+7-center3=8+7-13=2。

题3:稍微调整上题,若center2在a,对称半径为8,求完整的字符串和center3的对称半径。

答:
字符串为
center3=center2*2-center=7*2-4=10。对称半径为center2+8-center3=7+8-10=5。这样对吗?
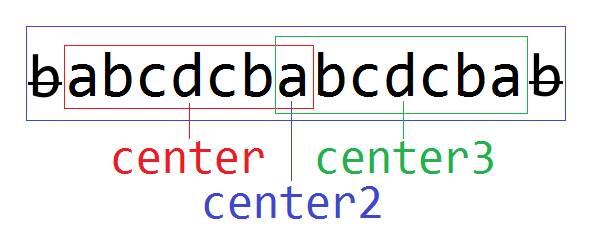
看起来半径不正确!应该同center一样都是4。问题出在哪里呢?明明用的是跟题2一样的公式啊!因为题2跟题3情况不同。题2 center左边超出了center2的对称范围;而题3 center左边没超出center2的对称范围。
center3的半径确定。
题4:同样,center在x,半径为2,center2在a,半径为5。求完整的字符串和center3半径。
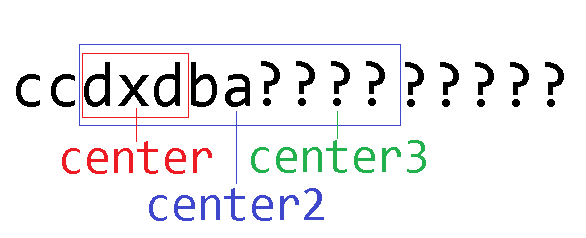
答:根据center2的对称性补全center2范围内的字符。又因为center2的对称半径为5而不是6,索引11位的字符不是c。
所以center3的半径就是2了吗?不一定哦!因为我们只知道索引11位的字符不是c,但它可能是b,这样就与索引7位的b匹配,对称半径达到3。同样地,我们也不知道索引12位的字符是什么。
所以,在center和center2的左边界重合时,我们只知道center3半径的最小值。
根据这三道例题,我们已经总结出回文字符的半径性质:
- 当center1范围左超center2范围(简称左超),center3的半径可由计算得出,为确切值。
- 当center1范围内含于center2范围(简称内含),center3的半径等于其关于center2的对称点半径,为确切值。
- 当center1左边界与center2左边界重合(简称接边),center2半径大于等于其关于center2的对称点半径,值不确定。
在情况1、2中,求的是确切值,所以即使center3内含于多个对称范围,每个对称范围求出的半径都一定是一样的。在情况3中,所有对称范围的计算值的最大值是center3半径的最小值。
基本代码
下面给出基本代码。
[code lang=”java”]
public static int getPalindromeLength(String s)
{
if (s.length() == 0)
return 0;
StringBuilder sb = new StringBuilder(s.length() * 2 + 1);
sb.setLength(sb.capacity());
for (int i = 0; i < s.length(); i++)
sb.setCharAt(i * 2 + 1, s.charAt(i));
s = sb.toString();
int[] radii = new int[s.length()];
for (int center = 0; center < s.length() – 1; center++) // O(n)
{
boolean notSure = true;
// 检查center是否在某个对称区域的右半边
for (int center2 = center – 1; center2 >= center / 2; center2–)
{
if (center2 + radii[center2] > center) // center在以center2为中心的对称区域的右半边
{
int c1 = center2 * 2 – center;
assert c1 >= 0;
if (c1 – radii[c1] < center2 – radii[center2])// 左超,半径确定
{
radii[center] = center2 + radii[center2] – center;
notSure = false;
break;
}
else if (c1 – radii[c1] > center2 – radii[center2]) // 内含,半径确定
{
radii[center] = radii[c1];
notSure = false;
break;
}
else
// 接边,半径可能变化
radii[center] = Math.max(radii[c1], radii[center]);
}
}
if (notSure)
{
// ccxbabxbabxcc
// 0123456789012
/*
* 索引6的x关于索引4的a对称,根据索引2的x得对称半径1。 但实际上索引6的x是整个字符串的对称中心。
*/
int r = radii[center];
while (center – r >= 0 && center + r < s.length() && s.charAt(center – r) == readChar(s, center + r))
r++;
radii[center] = r;
}
}
int maxRadius = radii[0];
for (int i = 0; i < radii.length; i++)
maxRadius = Math.max(maxRadius, radii[i]);
return (maxRadius – 1);
}
private static char readChar(String s, int index)//这个方法可用来查看计算复杂度
{
System.out.println("读取字符" + index);
return s.charAt(index);
}
[/code]
现在分析复杂度,令比较运算为耗时间的操作。该代码通过notSure变量,仅当i关于center2的对称点接边的时候才读取字符来比较。前面性质分析中说的是左侧接边,根据对称性也是右侧接边。进入if (notSure)分支后继续读取更右边的字符,然后记录在radii里。以后,从radii里读就可以了。建议亲手运行代码看看,会发现程序不会重读前面读过的字符,不会读了012345,然后又读2345。既然程序只读取字符2n次,那么比较进行了n次,所以时间复杂度是O(n)。
网上很多代码与上面的代码不太一样,有id、mx什么的,尤其有一个变量记录什么最右边的位置,不太好懂。读者如果理解了上面的基本代码,那么可以再看下下面的变形代码,变形代码与网上的代码比较像。变形代码的复杂度同样是O(n)。
[code lang=”java” title=”变形代码”]
public static int getPalindromeLength2(String s)
{
if (s.length() == 0)
return 0;
StringBuilder sb = new StringBuilder(s.length() * 2 + 1);
sb.setLength(sb.capacity());
for (int i = 0; i < s.length(); i++)
sb.setCharAt(i * 2 + 1, s.charAt(i));
s = sb.toString();
int[] radii = new int[s.length()];
int rCenter2 = 0;// 右边界最大的c
for (int i = 0; i < s.length() – 1; i++) // O(n)
{
// 检查center是否在某个对称区域的右半边
if (rCenter2 + radii[rCenter2] > i) // i在以center2为中心的对称区域的右半边
{
int c1 = rCenter2 * 2 – i;
assert c1 >= 0;
if (c1 – radii[c1] < rCenter2 – radii[rCenter2])// 左超,半径确定
radii[i] = rCenter2 + radii[rCenter2] – i;
else
// 不左超。但如果接边,半径可能变化
radii[i] = radii[c1];
}// 如果右最大的c都不包括i,那么其他c更不会包括了。
if (i + radii[i] == rCenter2 + radii[rCenter2])// 接边
{
int r = radii[i];
while (i – r >= 0 && i + r < s.length() && s.charAt(i – r) == readChar(s, i + r))
r++;
radii[i] = r;
// 接边后超右边比较,半径可能更大!
if (i + radii[i] > rCenter2 + radii[rCenter2])
rCenter2 = i;
}
}
int maxRadius = radii[0];
for (int i = 0; i < radii.length; i++)
maxRadius = Math.max(maxRadius, radii[i]);
return (maxRadius – 1);
}
[/code]
参考资料
xiangzhai. 最长回文子字符串 第二部. . 2014-02-14 [2015-02-06].References
- 半径大于等于1。↑