向量复习
2019年2月26日向量的坐标表示法
令点a的坐标为\((x_0,y_0)\),点b的坐标为\((x_1,y_1)\),则
\[\begin{equation}
\vec{ab}=\overrightarrow{(x_1-x_0,y_1-y_0)}
\label{坐标表示法}
\end{equation}\]
向量的模
向量的模表示向量的大小,记为\(|\boldsymbol{a}|\) 或\(|\vec{a}|\)。[1]模是绝对值在二维和三维空间的推广,可以认为是向量的长度。推广到高维空间中称为范数(norm)。[2](另见《median, mean, mode as minimizers》)
模为1的向量叫单位向量。向量\(\vec{a}\)的单位向量为\(\frac{\vec{a}}{|\vec{a}|}\)。
例:\(\vec{a}=\overrightarrow{(3,4)}\),求其单位向量\(\vec{a_0}\)。
\[
\vec{a_0}=\frac{\vec{a}}{|\vec{a}|}=\frac{\overrightarrow{(3,4)}}{|(3,4)|}=\frac{\overrightarrow{(3,4)}}{\sqrt{3^2+4^2}}=\frac{\overrightarrow{(3,4)}}{5}=\overrightarrow{(0.6,0.8)}
\]
向量点积
向量点积,又称数量积,是向量进行点乘运算的结果。相当于两个数相乘,乘出来的结果叫做积。
两个向量\(\vec{a}=(a_1, a_2, \cdots, a_n)\)和\(\vec{b}=(b_1, b_2, \cdots, b_n)\)的点积有如下多种定义:
\[\begin{equation}
\vec{a}\cdot \vec{b}= \sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n
\label{代数定义}
\end{equation}\]
\[\begin{equation}
\vec{a}\cdot \vec{b}= \det\left(\vec{a}^T\vec{b}\right)
\label{矩阵定义}
\end{equation}\]
注,矩阵相乘的结果始终为矩阵,1*1的矩阵不是标量,所以这里需要对1*1矩阵求行列式,得出标量。不严谨的文献或作者往往省去最后一句行列式运算。
\[\begin{equation}
\vec{a}\cdot \vec{b}= \left|\vec{a}\right| \left|\vec{b}\right| \cos \theta \qquad \theta\text{为}\vec{a}\ \vec{b}\text{的夹角}
\label{几何定义}
\end{equation}\]
以上\(\eqref{代数定义}\)为代数定义,\(\eqref{矩阵定义}\)为\(\eqref{代数定义}\)的矩阵改写,\(\eqref{几何定义}\)为几何定义。
若要求两向量的夹角,可把公式\(\eqref{几何定义}\)变换为
\[\begin{equation}
\cos \theta= \frac{\vec{a}\cdot \vec{b}}{ \left|\vec{a}\right| \left|\vec{b}\right|}
\label{cos}
\end{equation}\]
求投影向量的长度
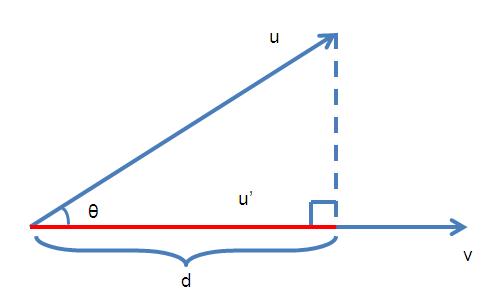
给定一个向量\(\vec{u}\)和\(\vec{v}\),求\(\vec{u}\)在\(\vec{v}\)上的投影向量,如下图。
令\(\vec{u}\)在\(\vec{v}\)上的投影向量为\(\vec{u’}\),且\(\vec{u}\)和\(\vec{v}\)的夹角为\(\theta\)。从\(\vec{u}\)的末端做\(\vec{v}\)的垂线,那么d就是\(\vec{u’}\)的长度,即\(\left|\vec{u’}\right|\)。
\[\begin{align*}
d=& \left| \vec{u’} \right| = \left|\vec{u} \right| \cos \theta \qquad \text{应用公式}\eqref{cos}\\
=& \left|\vec{u} \right| \times \frac{\vec{u}\cdot \vec{v}}{ \left|\vec{u}\right| \left|\vec{v}\right|}=\frac{\vec{u}\cdot \vec{v}}{ \left|\vec{v}\right|}
\end{align*}\]
所以,向量\(\vec{u}\)在\(\vec{v}\)上的投影长度为
\[
d=\frac{\vec{u}\cdot \vec{v}}{ \left|\vec{v}\right|}
\]
如果\(\vec{u}\)于\(\vec{v}\)的夹角大于90度,则距离为负,需要取绝对值,所以一般化的公式为
\[\begin{equation}
d=\left|\frac{\vec{u}\cdot \vec{v}}{ \left|\vec{v}\right|}\right|
\label{向量投影长度}
\end{equation}\]
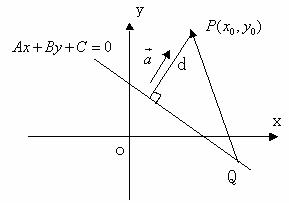
求点到直线的距离
已知直线l: Ax+By+C=0和点P \((x_0,y_0)\),d为点P到直线l的距离。直线的方向向量为\(\overrightarrow{(B,-A)}\),则其法向量\(\vec{a}=\overrightarrow{(A,B)}\)。又设点Q \((x_1,y_1)\)为直线上的任一点,故有\(Ax_1+By_1+C=0\)(如图所示)
变换问题为,求向量\(\overrightarrow{QP}\)在\(\vec{a}\)上的投影长度。
根据公式\(\eqref{坐标表示法}\),\(\overrightarrow{QP}=\overrightarrow{(x_0-x_1,y_0-y_1)}\)
根据公式\(\eqref{向量投影长度}\),
\[\begin{align*}
d=& \left|\frac{\overrightarrow{QP}\cdot \vec{a}}{\left | \vec{a} \right |}\right| \\
=& \left|\frac{\overrightarrow{(x_0-x_1,y_0,y_1)}\cdot \overrightarrow{(A,B)} }{\left|\overrightarrow{(A,B)} \right| }\right| \\
=& \left|\frac{A(x_0-x_1)+B(y_0-y_1) }{\sqrt{A^2+B^2}}\right| \\
=& \left|\frac{Ax_0+By_0+(-Ax_1-By_1)}{\sqrt{A^2+B^2}}\right| \\
=& \left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|
\end{align*}\]
若用公式\eqref{矩阵定义}把直线公式改写为矩阵点积的形式,则直线表示为\(\det{(\vec{w}^T\vec{x}+\vec{b})}=0\)。任意一点到该直线的距离为
\[
d=\frac{\left|\vec{w}^Tx+b \right|}{\left \| \vec{w} \right \|}
\]
这里分子的竖线表示取绝对值,分子的双竖线表示范数。
参考资料
- 蕭文達. 第四章 向量. 朝陽科技大學. [2019-02-26].
- zdd. 向量投影. 博客园. 2010-08-03 [2019-02-26].
- 杨胜万. 谈“点到直线距离公式”的向量推导方法. 贵州省黄平县旧州中学. 2007-11-22 [2019-02-26].
- 耳东陈. 零基础学SVM—Support Vector Machine(一). 朝陽科技大學. 2018-05-07 [2019-02-26].
References
- . 第一节 向量及其线性运算. 西安建筑科技大学. [2019-02-26].↑
- . 向量的模. 百度百科. [2019-02-26].↑