游戏《太阳帝国的原罪》里，瓦萨里种族可以建造相位跳跃稳定器，飞船可以直接从一个有相位跳跃稳定器的星球跳跃到另一个有相位跳跃稳定器的星球，无需现有路线。

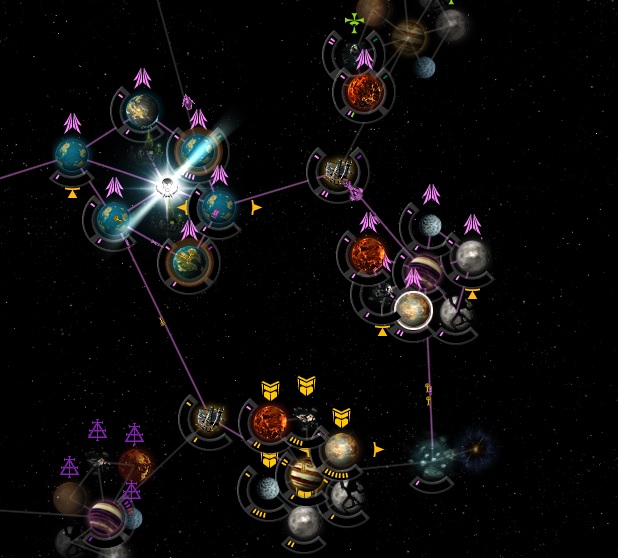
如图1，粉色是我的星球。如何添加两个相位跳跃稳定器，能够最大程度地减少我方飞船在各个星球之间的飞行距离？

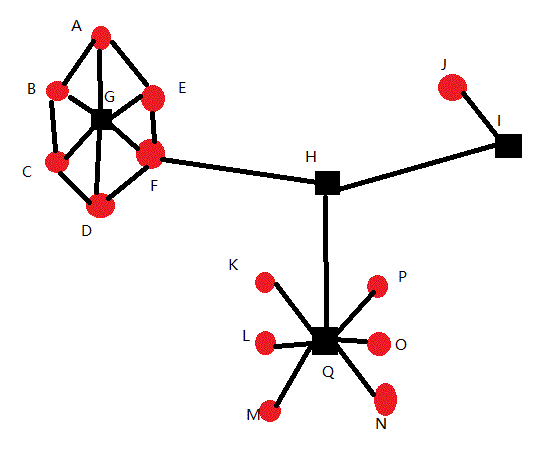
把上图数学化，如图2，红色是可以添加相位跳跃稳定器的星球，黑色是不能添加相位跳跃稳定器的星球。

解法

似乎除了穷举法没有更好的办法。于是我用Mathematica实现。

(* 定义可添加边的顶点和不能添加边的顶点 *)
colonizableVertices = {a, b, c, d, e, f, j, k, l, m, n, o, p};
noncolonizableVerticex = { g, h, i, q};


edges = {a <-> g, b <-> g, c <-> g, d <-> g, e <-> g, f <-> g,
               a <-> b, b <-> c, c <-> d, d <-> f, f <-> e, e <-> a,
                 f <-> h, h <-> i, i <-> j,
                 h <-> q,
                 q <-> k, q <-> l, q <-> m, q <-> p, q <-> o, q <-> n
  }

(* 穷举新的边，排除已存在的边 *)
possibleNewEdges = UndirectedEdge[#[[1]], #[[2]]] & /@ Subsets[colonizableVertices, {2}];
possibleNewEdges = Select[possibleNewEdges, ! (MemberQ[edges, #[[1]] <-> #[[2]]] || MemberQ[edges, #[[2]] <-> #[[1]]]) &]

(* 定义新函数，接受新的边，获取图，然后计算图的距离之和 *)
getNewTotalDistance[newEdge_] := Module[{g, t},
  (graph = Graph[Join[colonizableVertices, Style[#, Red] & /@ noncolonizableVerticex], Union[edges, {newEdge}]];
   total = Total[GraphDistanceMatrix[graph], 2];
   Return[{total, newEdge}];
   )]

SortBy[Map[getNewTotalDistance, possibleNewEdges], First]

最后输出如图3，可见添加bk,bl,bm,bn,bo,bp都能使距离之和下降到728。