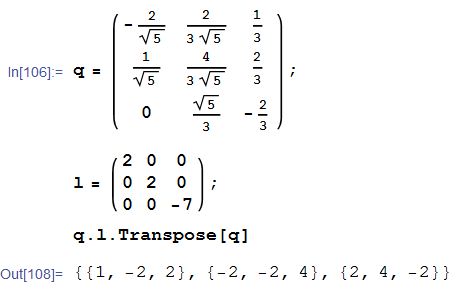零基础求矩阵特征值和特征向量
2014年10月22日
[mathjax]
虽然说零基础,但你还是不得不掌握行列式的求法。本文的矩阵都是低阶的,不讲述一般性的、N阶矩阵的解法。
特征值和(右)特征向量的定义
假设 A 是一个方阵。若一个非[latex]\vec{0}[/latex]的向量[latex]\vec{x}[/latex]满足下面的等式
[latex]A\vec{x}=\lambda\vec{x}[/latex]
则[latex]\vec{x}[/latex]为矩阵A的(右)特征向量,而[latex]\lambda[/latex]是矩阵 A 相对于[latex]\vec{x}[/latex]的特征值。[5]一个特征值对应的特征向量有无穷个。
(左特征向量是乘在矩阵左边的特征向量,即[latex]\vec{x}A=\lambda\vec{x}[/latex]。左特征向量不常见。)
求特征值和特征向量
从定义得以下变换
$$
\begin{align*}
A\vec{x} &=\lambda\vec{x} \\
A\vec{x}-\lambda\vec{x} &= 0\\
(A-\lambda E) \vec{x} &=0 \\
\end{align*}
$$
有定理:
于是我们获得特征值和特征向量的求法:
令[latex]\det(A-\lambda E)=0[/latex](A为矩阵,E为单位矩阵)的[latex]\lambda[/latex]为矩阵A的特征值(有多个)。
对于N阶矩阵,有N个特征值,可能重复。对于每个特征值[latex]\lambda_i[/latex],求令[latex](A-\lambda_iE)X=0[/latex]的[latex]X_i[/latex],为[latex]\lambda_i[/latex]对应的特征向量。特征向量不得为零向量。特征向量有无穷个。
例1
$$A=\begin{bmatrix}
1 & -2 & 2\\ -2 & -2 & 4\\ 2 & 4 & -2
\end{bmatrix}$$
求A的特征值和特征向量。[1]
解:
$$\det(A-\lambda E)=\det \left ( \begin{bmatrix}
1-\lambda & -2 & 2\\
-2 & -2-\lambda & 4\\
2 & 4 & -2-\lambda
\end{bmatrix} \right )=0$$
$$\begin{align*}
(1-\lambda)(\lambda+2)^2-16-16-16(1-\lambda)+4(-2-\lambda)+4(2+\lambda) &= 0\\
(2-\lambda)^2(7+\lambda) &=0
\end{align*}$$
(如果把上式改写为以[latex]\lambda[/latex]的降幂排列的多项式,则称为矩阵A的特征多项式,即[latex]-\lambda^3-3\lambda^2+24\lambda-28[/latex])。
求得 [latex] \lambda_1=\lambda_2=2[/latex]或[latex]\lambda_3=-7[/latex]。
所以矩阵A的特征值是2、2、-7。接下来对于每个特征值,求其对应的特征向量。
当[latex]\lambda=2[/latex]时,
$$
(A-2E)X=\begin{bmatrix}-1 & -2 & 2\\ -2 & -4 & 4\\ 2 & 4 & -4\end{bmatrix}
\begin{bmatrix}a\\ b\\ c\end{bmatrix}=0
$$
$$\left\{\begin{matrix}
-a-2b+2c=0\\ -2a-4b+4c=0\\ 2a+4b-4c=0
\end{matrix}\right.
\quad
\Rightarrow
a=-2b+2c
$$
[2](视b、c为常数)
特征向量[latex]X=\begin{bmatrix}-2b+2c\\ b\\ c\end{bmatrix}=b\begin{bmatrix}-2\\ 1\\ 0\end{bmatrix}
+c\begin{bmatrix}2\\ 0\\ 1\end{bmatrix}[/latex]。
或改写为[latex]X=\begin{bmatrix}-2b+2c\\ b\\ c\end{bmatrix}=k_1\begin{bmatrix}-2\\ 1\\ 0\end{bmatrix}
+k_2\begin{bmatrix}2\\ 0\\ 1\end{bmatrix}[/latex]([latex]k_1, k_2[/latex]不同时为0)。
当[latex]\lambda=-7[/latex]时,
[latex](A+7E)X=\begin{bmatrix}8 & -2 & 2\\ -2 & 5 & 4\\ 2 & 4 & 5\end{bmatrix}
\begin{bmatrix}a\\ b\\ c\end{bmatrix}=0[/latex]
[latex]\left\{\begin{matrix}
8a-2b+2c=0\\ -2a+5b+4c=0\\ 2a+4b+5c=0
\end{matrix}\right.
\quad
\Rightarrow
\left\{\begin{matrix}
a=-\frac{1}{2}c\\ b=-c
\end{matrix}\right. [/latex]
(视c为常数)
特征向量[latex]X=\begin{bmatrix}-\frac{1}{2}c\\ -c\\ c\end{bmatrix}=-2c\begin{bmatrix}1\\ 2\\ -2\end{bmatrix}[/latex]。
或改写为[latex]X=\begin{bmatrix}-\frac{1}{2}c\\ -c\\ c\end{bmatrix}=k\begin{bmatrix}1\\ 2\\ -2\end{bmatrix}[/latex](k不为0)。
特征分解
按照定义(?),有[latex]AQ=QL[/latex],两边同乘Q的逆矩阵,得[latex]A=QLQ^{-1}[/latex]。
Q是一个矩阵,其每一列以此是A的特征向量的分量。L是一个矩阵,其对角线依次是A的特征值;其他元素为0。
例1
继续例1,
[latex]Q=\begin{bmatrix}-2 & 2 & 1\\ 1 & 0 & 2\\ 0 & 1 & -2\end{bmatrix}[/latex]
[latex]L=\begin{bmatrix}2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & -7\end{bmatrix}[/latex]。
注意特征值和特征向量要一一对应。
这里不要求计算Q的逆矩阵,借助数学软件(如Mathematica),得
获得了我们一开始的矩阵A,证明我们的特征向量和特征值是正确的。
特别的,如果矩阵A是对称矩阵([latex]A=A^t[/latex]),则有Q使得[latex]A=QLQ^{-1}=QLQ^t[/latex],即Q的转置等于Q的逆。
易证
[latex]Q=\begin{bmatrix}-2 & 2 & 1\\ 1 & 0 & 2\\ 0 & 1 & -2\end{bmatrix}[/latex]
时,[latex]QLQ^t\neq A[/latex],于是我们重新求使该式成立的Q。
这里要用到格拉姆-施密特正交化。[3]
设[latex]v_2=(-2,1,0),\quad v_3=(2,0,1), \quad v_1=(1,2,-2)[/latex],设[latex]\beta_1,\beta_2,\beta_3[/latex]为[latex]v_1, v_2, v_3[/latex]正交化后的向量。Q将由[latex]\beta_1,\beta_2,\beta_3[/latex]组成。这里我故意没有按顺序对[latex]v_1, v_2, v_3[/latex]编号,读者可以按不同的顺序对[latex]v_1, v_2, v_3[/latex]编号,看能否求出Q。注意,Q并不是唯一的。
格拉姆-施密特正交化过程如下:[4]
[latex]\beta_1=v_1=(1,2,-2)[/latex]
[latex]\begin{align*}
\beta_2 &= v_2-\operatorname{Projection}(v2,\beta_1)\\
&= (-2,1,0)-\frac{(-2,1,0)\cdot (1,2,-2)}{(1,2,-2).(1,2,-2)}(1,2,-2)\\
&= (-2,1,0)- (0,0,0) \\
&= (-2,1,0)
\end{align*}[/latex]
[latex]\begin{align*}
\beta_3 &= v_3-\operatorname{Projection}(v3,\beta_1)-\operatorname{Projection}(v3,\beta_2)\\
&= (2,0,1)-\frac{(2,0,1).(1,2,-2)}{(1,2,-2).(1,2,-2)}(1,2,-2) -\frac{(2,0,1)(-2,1,0)}{(-2,1,0).(-2,1,0)}(-2,1,0)\\
&= (2,0,1)- (0,0,0)-(\frac{8}{5},-\frac{4}{5},0)\\
&= (\frac{2}{5},\frac{4}{5},1)
\end{align*}[/latex]
然后把[latex]\beta_1,\beta_2,\beta_3[/latex]正规化,变成单位向量。
[latex]\beta_1^{‘}=\operatorname{Normalize}(\beta_1)=(\frac{1}{3},\frac{2}{3},-\frac{2}{3})[/latex]
[latex]\beta_2^{‘}=\operatorname{Normalize}(\beta_2)=(-\frac{2}{\sqrt{5}},\frac{1}{\sqrt{5}},0)[/latex]
[latex]\beta_3^{‘}=\operatorname{Normalize}(\beta_3)=(\frac{2}{3 \sqrt{5}},\frac{4}{3 \sqrt{5}},\frac{\sqrt{5}}{3})[/latex]
所以
[latex]Q=\begin{bmatrix}-\frac{2}{\sqrt{5}} & \frac{2}{3 \sqrt{5}} & \frac{1}{3}\\\frac{1}{\sqrt{5}} & \frac{4}{3 \sqrt{5}} & \frac{2}{3}\\0 & \frac{\sqrt{5}}{3} & -\frac{2}{3}\end{bmatrix}[/latex]
(用Mathematica)验证Q是否正确:
结果为A,说明我们的计算是正确的。
参考资料
- 矩阵的特征值与特征向量, 5-特征值.pps
- 提要 67 :特徵向量的解法( 二)– 特徵根有重根, Summary_067.pdf
- Know eigenvalues, get Q of A=QLQ′
- The Gram-Schmidt Algorithm
- Eigenvectors and Eigenvalues 特征向量和特征值
- Inverse Matrices 反矩阵
本文依照知识共享-署名-相同方式共享3.0协议发布